M.C. Escher: The Mathematical Artist

by Quinn Polaski, Contributing Writer

Pictures from google.com

Editor’s note: This article has been inspired by the recent exhibits in St. Louis.

Maurits Cornelius (M.C.) Escher was a revolutionary Dutch man who brought the two fields of art and math together. During the 20th century, Escher created over 400 lithographs and 200 sketches. Lithography is the use of oil and water to create drawings, and it bears close resemblance to painting. Although you may not recognize his name, some of his most famous work has been seen by most of us. For example, his piece “Relativity” used his mathematical skills to draw a room with many staircases that go up, down, and sideways from many XYZ positions.

Born in 1898, M.C. started using geometry and the principles of graph theory to create art. His early work contained sketches of people, faces, and animals, especially birds. When M.C. left his home and went to Italy, he started to draw more basic shapes and use geometry to create some wacky feats of engineering. He called some of his pieces “impossible” because the buildings and layouts in them could not be constructed. For example, in his lithograph “Cycle,” the running men emerge from an orderly home and descend into a topsy-turvey chaos, but this chaos itself gives rise to the very order from which the figures emerge.

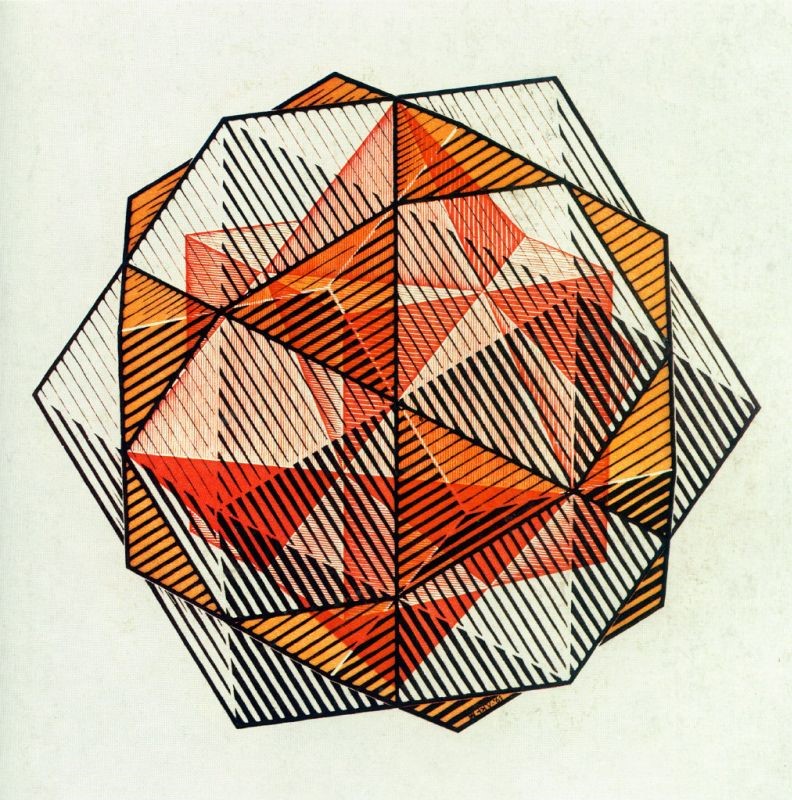
Because of the spread of Fascism, M.C. had to leave Italy. In my opinion, Escher’s best work is from his Belgium time. He took basic shapes like parallelograms and triangles then made them tessellate to fill in a page; then he could go back and change these shapes into animals such as birds and fish. Famous pieces such as “Horseman Tessellation” and “Hexagon Fish Vignette” show his familiarity with graphing mobility, movement like transformation, translation, and rotations.  Escher was also interested in polyhedra, solid 3D figures. There are five polyhedra that Escher involved in his art. “The Platonic Solids” are described as polyhedra that have congruent regular polygons as faces, the most common is the cube. The others are tetrahedron, octahedron, dodecahedron, and icosahedron.

Escher, like many other famous artists, had problems with his work and feared how others would perceive it. Despite all this interpretive artwork, Escher’s son quoted that his father “denied any ability to understand or do mathematics.” This doesn’t make much sense until you look at the more artistic side of his work, rather than try to rationalize it with mathematics. Escher wouldn’t need to understand a high-level mathematical concept such as knot theory to make impossible art like the Mobius Strip. If you are curious about knot theory please reach out to McKendree’s own Dr. Dye, as she is very proficient.

Escher designed some very fascinating art. When his fame reached an atmospheric level in the 1950s and 1960s, many mathematicians came to Escher to talk about his work, education, and why he was so interested. He stated, “for me it remains an open question whether [this work] pertains to the realm of mathematics or to that of art.”